E資格のお勉強(オンライン講座 1/6) 応用数学

はじめに
第一章:線形代数
第二章:確率・統計
第三章:情報理論
ご紹介: E資格対策講座ラビットチャレンジについて

はじめに

ディープラーニングＥ資格(JDLA主催)のオンライン講座(ラビットチャレンジ)を受講したときの学習記録になります。

E資格の一通りの科目をカバーしています。学習の参考にしてください。

科目一覧

応用数学　←ココ
機械学習
深層学習(day1)
深層学習(day2)
深層学習(day3)
深層学習(day4)

第一章:線形代数

固有値分解とは

特異値分解とは
正方形以外のものを固有値分解する方法

このような特殊な単位ベクトルがあるならば特異値分解ができる
UやVは直交行列になる

特異値の求め方

例題

以下のような行列がある。

$M=\left( \begin{array}{ccc} 1 & 2 & 3 \\ 3 & 2 & 1 \end{array} \right)$

これに、自分を転置した行列を掛ける。出来上がる正方形の行列は、対称形になる。

$MM^T =\left( \begin{array}{ccc} 1 & 2 & 3 \\ 3 & 2 & 1 \end{array} \right)\left( \begin{array}{ccc} 1 & 3 \\ 2 & 2 \\ 3 & 1 \end{array} \right)=\left( \begin{array}{ccc} 14 & 10 \\ 10 & 14 \end{array} \right)$

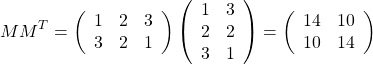
これを固有値分解して

$\left( \begin{array}{ccc} 14 & 10 \\ 10 & 14 \end{array} \right) =\left( \begin{array}{ccc} 1\sqrt{2} & -1\sqrt{2} \\ 1\sqrt{2} & 1\sqrt{2} \end{array} \right)\left( \begin{array}{ccc} 24 & 0 \\ 0 & 4 \end{array} \right)\left( \begin{array}{ccc} 1\sqrt{2} & -1\sqrt{2} \\ 1\sqrt{2} & 1\sqrt{2} \end{array} \right)^{-1}$

逆の場合。つまり $M^T$ が先に来る場合

$M^TM =\left( \begin{array}{ccc} 1 & 3 \\ 2 & 2 \\ 3 & 1 \end{array} \right)\left( \begin{array}{ccc} 1 & 2 & 3 \\ 3 & 2 & 1 \end{array} \right)=\left( \begin{array}{ccc} 10 & 8 & 6 \\ 8 & 8 & 8 \\6 & 8 & 10\end{array} \right)$

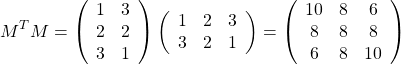
これも同様に、出来上がる正方形の行列は、対称形になる。

これを固有値分解して

$\left( \begin{array}{ccc} 10 & 8 & 6 \\ 8 & 8 & 8 \\6 & 8 & 10\end{array} \right)=\left( \begin{array}{ccc} 1\sqrt{3} & 1\sqrt{2} & 1\sqrt{6} \\ 1\sqrt{3} & 0 & -2\sqrt{6} \\1\sqrt{3} & -1\sqrt{2} & 1\sqrt{6}\end{array} \right)\left( \begin{array}{ccc} 24 & 0 & 0 \\ 0 & 4 & 0 \\0 & 0 & 0\end{array} \right)\left( \begin{array}{ccc} 1\sqrt{3} & 1\sqrt{2} & 1\sqrt{6} \\ 1\sqrt{3} & 0 & -2\sqrt{6} \\1\sqrt{3} & -1\sqrt{2} & 1\sqrt{6}\end{array} \right)^{-1}$

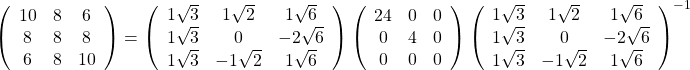
特異値分解の応用例

ある白黒2色の画像を、濃淡情報を数字として捉えた2次元の数字の配列と考えることができる。
さらに、配列の固有値から特定の情報だけ取捨選択すると、解像度を下げたような画像ができる。たとえば左側の画像から特異値の128だけを残すと、右側のようになる。

上記のように特異値分解を用いれば、元の画像の情報量を減少させて表示したり、複数の画像の特徴の共通点を見出すことに応用することができる。これは実際によく使われている。

第二章:確率・統計

ベイジアン確率

例題

共分散

例題

ベルヌーイ分布
・コインを投げたとき、表が出る(x=1)場合は $\mu$ である。裏が出る(x=0)場合は $1-\mu$ である。
・表と裏の出る確率が同じ(つまり $\mu$ =0.5)でなくても、使える。

$P(x|\mu)=\mu^x(1-\mu)^{1-x}$

二項分布
・ベルヌーイ分布の多試行版

$P(x|\lambda,n)=\frac{n!}{x!(n-x)!}\lambda^x(1-\lambda)^{n-x}$

ガウス分布

$N(x;\mu,\sigma^2)=\sqrt{\frac{1}{2\pi\sigma^2}}\exp(-\frac{1}{2\sigma^2}(x-\mu)^2)$

第三章:情報理論

・自己情報量
たとえば16個の事象が起こりうるとき、
自己情報量: $I(x) = \log W(x) = \log(16) = 4$ ※ただし対数の底を2で取った場合
また、同じことを事象の確率で求めることができる。
その事象が $1/16$ の確率で起こる場合、自己情報量: $I(x) = -\log P(x) = -\log (1/16) = 4$
※単位について
対数の底が2のとき，単位はビット(bit)
対数の底がネイピアのeのとき，単位は(nat)

・シャノンエントロピー
自己情報量の期待値

・カルバック・ライブラー・ダイバージェンス
同じ事象・確率変数における異なる確率分布P,Qの違いを表す

・交差エントロピー
次章でまとめる。

ご紹介: E資格対策講座ラビットチャレンジについて

Ｅ資格を受けるには、対象の講座の修了が必要です。

ラビットチャレンジは「現場で潰しが効くディープラーニング講座」の通学講座録画ビデオを編集した教材を活用したコースです。

質問等のサポートはありませんが、E資格受験のための最安（2020年5月時点）の講座の一つです。

詳細は以下のリンクからご確認ください。