E資格のお勉強(オンライン講座 3/6) 深層学習(day1)

  1. ホーム
  2. 未分類
  3. E資格のお勉強(オンライン講座 3/6) 深層学習(day1)

目次

はじめに

ディープラーニングＥ資格(JDLA主催)のオンライン講座(ラビットチャレンジ)を受講したときの学習記録になります。

E資格の一通りの科目をカバーしています。学習の参考にしてください。

科目一覧

  • 応用数学　
  • 機械学習　
  • 深層学習(day1) ←ココ
  • 深層学習(day2)
  • 深層学習(day3)
  • 深層学習(day4)

Section1: 入力層~中間層

  • 入力層のそれぞれの入力に関して、重みが掛け合わされて加算された値が第一の中間層のユニットに入力される。
  • 重みは 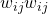w_{ij}w_{ij} は、入力 ii と 中間層ユニット jj に関してそれぞれ値が決定されている。(ネットワークのパラメータ)

確認テストの考察

・問題
ディープラーニングは、結局何をやろうとしているか2行以内で述べよ。また、次の中のどの値の最適化が最終目的か。全て選べ。（1分）
①入力値[ X] ②出力値[ Y]③重み[W]④バイアス[b]⑤総入力[u] ⑥中間層入力[ z]⑦学習率[ρ]
・答え
ある情報の集まりを分類する。
ある問題を解くこと。
③,④

Section2: 活性化関数

  • NN において、次の層への出力を決定する非線形の関数。
    • 非線形であることは NN にとって本質的に重要。
  • ON/OFF を次の層に強めに渡すのか、弱めに渡すのか、ということで、そこで人間らしさ的なものを出している。
  • 例1: シグモイド関数 11+e−x_{11}+e−x
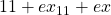
    • 0 ～ 1 の値をとる。
    • 絶対値が大きくなると、勾配が小さくなってしまう。→　勾配消失問題
    • ゼロにならない。 → スパース化できない。計算量が無駄に発生してしまう。
  • ReLU
    • 0(x<0),1(0<=x)0(x<0),1(0<=x)
    • 現世代では第一の選択肢となる関数 (必ずしも最適というわけではない)
    • プラスで」あれば勾配はゼロにはならない。
    • 0 をとることでスパース化のメリットがある。

確認テストの考察

・問題
次のネットワークを紙にかけ。入力層︓2ノード1層 中間層︓３ノード2層 出力層︓1ノード1層（5分）
・答え

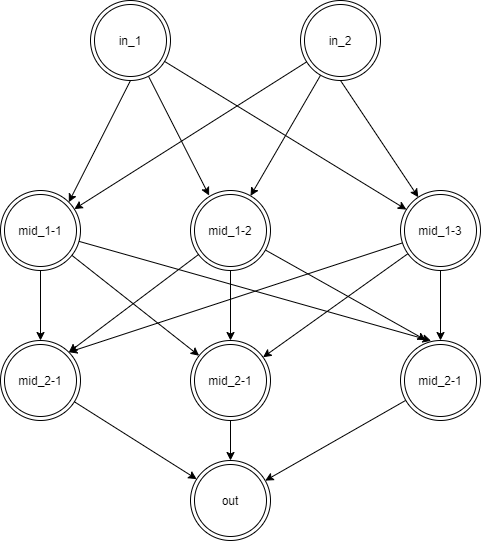
・問題
1-1のファイルから中間層の出力を定義しているソースを抜き出せ。（2分）
・答え

# 中間層出力
z = functions.relu(u)

・問題
線形と非線形の違いを図にかいて簡易に説明せよ。（2分）
・答え
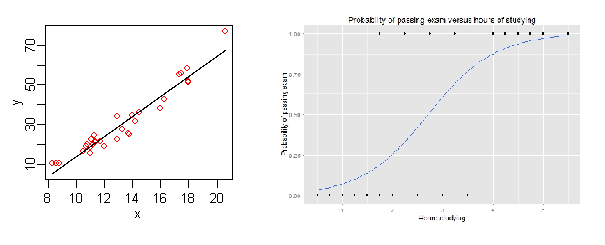
以下の図を参考にしてください。
機械学習において、モデルが線形か非線形かの違いについて。
線形: 既定関数\phi(x)が、1次である。
左図である。線で解けることを意味する。回帰の場合、目的変数:説明変数のグラフを書くと線になる。
非線形: それ以外の場合。例は右図である。

・問題
配布されたソースコードより該当する箇所を抜き出せ。（3分
・答え
# 中間層出力
z = functions.sigmoid(u)
print_vec(“中間層出力”, z)

Section3: 出力層

【誤差関数】

  • 二乗和誤差 12∑(yi−di)212∑(yi−di)2
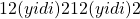
  • 分類問題に関してはクロスエントロピー関数を利用するのが普通。

【出力層の活性化関数】

  • 中間層と出力数で活性化関数を利用する目的が異なるので、同一である必要はない。
  • 回帰問題の場合: 恒等関数 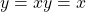y=xy=x / 誤差関数は二乗誤差
  • ロジスティック回帰: シグモイド関数 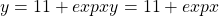y=11+exp−xy=11+exp−x / 誤差関数は交差エントロピー
  • 分類問題: ソフトマックス関数 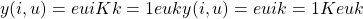y(i,u)=eui∑Kk=1euky(i,u)=eui∑k=1Keuk / 誤差関数は交差エントロピー

確認テストの考察

・問題
なぜ、引き算でなく二乗するか述べよ
下式の1/2はどういう意味を持つか述べよ（2分）
E_n(W) = 1/2\sum_{i=1}^{J} (y_j-d_j)^2 = 1/2||(y-d)||^2
・答え
符号を帳消しにするため。
微分すると出てくる2と相殺させて、計算式が見やすくなる。

・問題
①~③の数式に該当するソースコードを示し、一行づつ処理の説明をせよ。（5分）
f(i,u) = \frac{e^{u^i}}{\sum_{K=1}^{K}e^{u_k}}

def softmax(x):
    if x.ndim == 2: #入力が2次元の場合の対処
        x = x.T
        x = x -np.max(x, axis=0)
        y = np.exp(x) /np.sum(np.exp(x), axis=0)
        return y.T
    x = x -np.max(x) #オーバーフロー対策
    return np.exp(x) / np.sum(np.exp(x))
#ndim: 次元数。つまり何行の要素があるか。
#axis=0: 行方向
#axis=1: 列方向

Code language: PHP (php)

・答え
xは入力のデータを示す。
例えば1次元の配列を入力にしたとき、数式で示しているiは、出力の配列のi番目に該当する。まず全部の数にて、最大値を減算する。次に全部の数にて、総和で割る。
例えば2次元の配列を入力にしたとき、if文が判定され、xを転置して行方向での処理が行われる。まず全部の数にて、行方向の最大値を減算する。次に全部の数にて、行方向の総和で割る。最後に出力の際は、転置する。

・問題
①~②の数式に該当するソースコードを示し、一行づつ処理の説明をせよ。（5分
E_n(W) = -\sum_{i=1}^{I}d_i \log y_i
→交差エントロピー

def cross_entropy_error(d, y):
    if y.ndim== 1:
        d= d.reshape(1, d.size)
        y= y.reshape(1, y.size)
    # 教師データがone-hot-vectorの場合、正解ラベルのインデックスに変換
    if d.size== y.size:
        d= d.argmax(axis=1)
        batch_size= y.shape[0]
    return -np.sum(np.log(y[np.arange(batch_size), d] + 1e-7)) / batch_size

#np.argmax: 多次元配列の中の最大値の要素を持つインデックスを返す関数です。axisで軸の方向を指定可能。
#numpy.arange(start, stop, step): 連続した値を生成可能。start(3)のみの指定では、0<=n<3(0,1,2)になる。
#np.ndarray.size: 配列の要素数を取得

Code language: PHP (php)

・答え
one-hotでは不正解のラベルは０になる(=誤差は0)のため無視して良い。
訓練データの数に関係なく統一した指標が得られるようにbatch_sizeで割る
以下が戻り値で交差エントロピーとなる。
-np.sum(np.log(y[np.arange(batch_size), d] + 1e-7)) / batch_size
・考察
例題はミニバッチ対応版
ミニバッチ（小さな塊）：データの中から一部を選び出し、その一部のデータを全体の「近似」として利用
ポイント：one-hotでは不正解のラベルは０になる(=誤差は0)のため無視して良い。訓練データの数に関係なく統一した指標が得られるようにNで割る

#例: ミニバッチ対応版ではないシンプルなもの。ポイント:one-hot表現　正解ラベルだけ1、他は0（ラベルはt）
def cross_entropy_error(y, t) :
    delta = le-7
    return -np.sum(t*np.log(y+delta))
Code language: PHP (php)

Section4: 勾配降下法

  • 勾配降下法
    • 一回のパラメータ更新に訓練データすべてを利用する。
    • 計算量 (空間・時間) が訓練データ n に対して O(n)O(n) 必要となる。
  • 確率的勾配降下法(SGD)
    • サンプルのうち 1 つのデータごとにパラメータの更新を行う。
    • 学習結果はサンプルのデータ順に依存する。
    • 計算量と収束速度の面でメリットがある。
  • ミニバッチ勾配降下法
    • 狭義の確率的勾配降下法では、GPU等のSIMDのメリット等を生かせないため、ある程度の数のサンプルをまとめて1回のパラメータ更新に利用する。
    • 文脈によっては、SGD(確率的勾配降下法) に含める場合もある。
  • 訓練データ1周を「エポック」としてカウントする。

確認テストの考察

・問題
該当するソースコードを探してみよう。（1分）
・答え
network[key]  -= learning_rate * grad[key]
grad = backward(x, d, z1, y)

・問題
オンライン学習とは何か2行でまとめよ（2分）
・答え
オンライン学習とは学習データが入ってくるたびにその都度、新たに入ってきたデータのみを使って学習を行うもの。 
バッチ学習に対して、学習を行う際に1からモデルを作り直すのではなく、そのデータによる学習で今あるモデルのパラメータを随時更新していくと流れになる。

・問題
この数式の意味を図に書いて説明せよ。（3分）
w^{(t+1)}=w^{(t)}-\epsilon \delta E_t
・答え
E_tはランダムに分割したデータの集合(ミニバッチ)に属するサンプルの平均誤差である。
ここではt+1の時の重みWを求める。そのために、tの時の重みWから、E_tをwで微分した値と、学習率である\epsilonを掛けたものを減算している。

Section5: 誤差逆伝播法

  • 誤差(関数)をパラメータで微分した関数を利用し、出力層側から、ネットワークのパラメータ更新を行う。
  • 最小限の計算で、(数値微分ではなく) 解析的にパラメータの更新量を計算する手法。
  • 逆伝播をすることで、不要な再帰的計算（探索）を避けるという意味もある。

確認テストの考察

・問題
誤差逆伝播法では不要な再帰的処理を避ける事が出来る。既に行った計算結果を保持しているソースコードを抽出せよ。（3分）
・答え

def init_network():
# print("##### ネットワークの初期化 #####")
network = {}
nodesNum = 10
network['W1'] = np.random.randn(2, nodesNum)
network['W2'] = np.random.randn(nodesNum)
network['b1'] = np.random.randn(nodesNum)
network['b2'] = np.random.randn()
# print_vec("重み1", network['W1'])
# print_vec("重み2", network['W2'])
# print_vec("バイアス1", network['b1'])
# print_vec("バイアス2", network['b2'])

return network
Code language: PHP (php)

Appendix: 実装演習

キャプチャ

ご紹介: E資格対策講座 ラビットチャレンジについて

Ｅ資格を受けるには、対象の講座の修了が必要です。

ラビットチャレンジは「現場で潰しが効くディープラーニング講座」の通学講座録画ビデオを編集した教材を活用したコースです。

質問等のサポートはありませんが、E資格受験のための最安（2020年5月時点）の講座の一つです。

詳細は以下のリンクからご確認ください。